Python 语言实现六大查找算法

目录

• 一、顺序查找算法
• 二、折半查找算法
• 三、插补查找算法
• 四、哈希查找算法
• 五、分块查找算法
• 六、斐波那契查找算法
• 七、六种查找算法的时间复杂度

一、顺序查找算法

顺序查找又称为线性查找，是最简单的查找算法。这种算法就是按照数据的顺序一项一项逐个查找，所以不管数据顺序如何，都得从头到尾地遍历一次。顺序查找的优点就是数据在查找前，不需要对其进行任何处理(包括排序)。缺点是查找速度慢，如果数据列的第一个数据就是想要查找的数据，则该算法查找速度为最快，只需查找一次即可；如果查找的数据是数据列的最后一个(第几个)，则该算法查找速度为最慢，需要查找 n 次，甚至还会出现未找到数据的情况。

例如，有这样一组数据：10、27、13、14、19、85、70、29、69、27。如果想要查找数据 19，需要进行 5 次查找；如果想要查找数据 27，需要进行 10 次查找；如果想要查找数据 10，只需要进行 1 次查找。

从这个例子中可以看出，当查找的数据较多时，用顺序查找就不太合适，所以说顺序查找只能应用于查找数据较少的数据列。这个过程好比我们在抽屉里找笔，如下图所示。通常情况下我们会从上层的抽屉开始，一层一层地查找，直到找到笔为止，这个例子就是生活中典型的顺序查找算法。

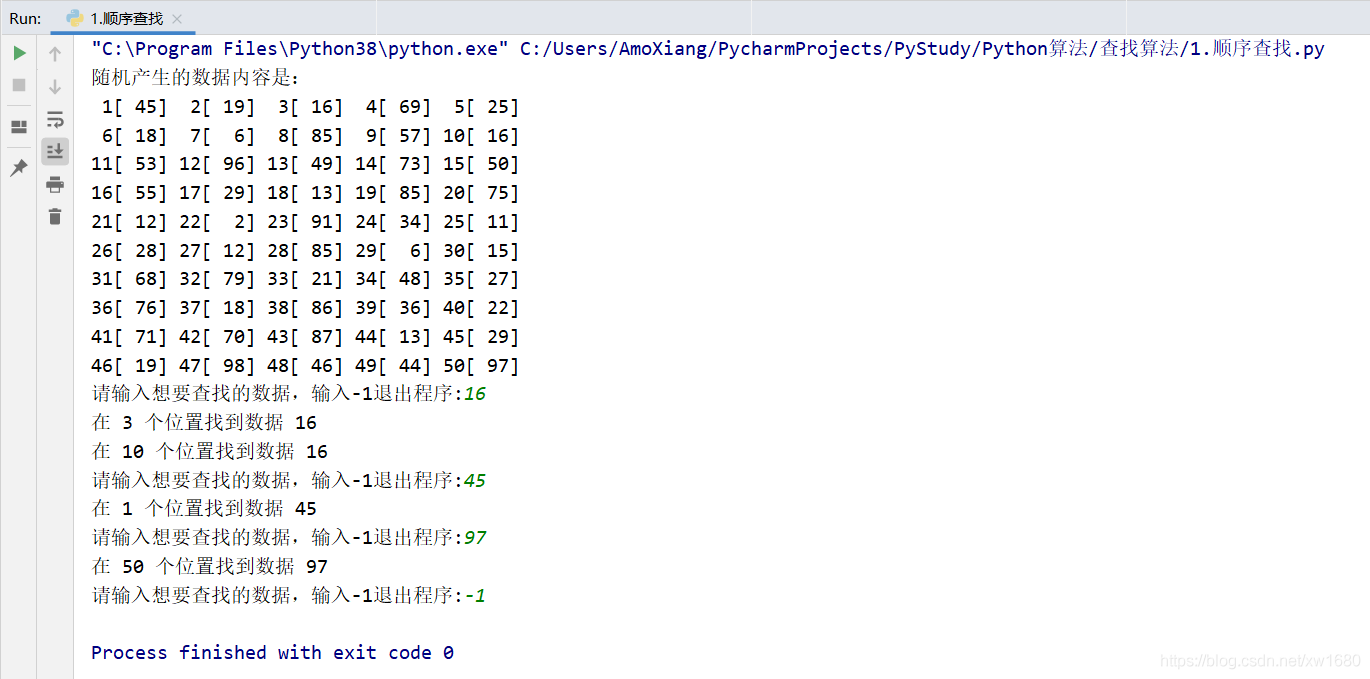
例如，随机从 1~100 之间生成 50 个整数，并将随机生成的这 50 个数显示出来，然后用顺序查找算法查找16、45、97这几个数据的位置。具体代码如下：

 import random # 导入随机数模块 num = 0 # 定义变量num # 使用列表推导式生成包含50个元素的列表 data = [random.randint(1, 100) for i in range(50)] print("随机产生的数据内容是：") for i in range(10): # 遍历行 for j in range(5): # 遍历列 # 按格式输出随机生成内容 print('%2d[%3d] ' % (i * 5 + j + 1, data[i * 5 + j]), end='') print('') while num != -1: # 循环输入 find = 0 # 比较次数 num = int(input("请输入想要查找的数据，输入-1退出程序:")) # 数据输入 for i in range(50): # 循环遍历50个随机数 if data[i] == num: # 判断输入数据和data数据是否相等 print("在", i + 1, "个位置找到数据", data[i]) # 输出找到的位置和数据内容 find += 1 # 比较次数加1 if find == 0 and num != -1: # 判断比较次数是否为0且输入数据是否为-1 print("没有找到", num, "此数据") # 提示没有找到数据

程序运行结果如下图所示：

二、折半查找算法

折半查找算法又称为二分查找算法，折半查找算法是将数据分割成两等份，首先用键值(要查找的数据)与中间值进行比较。如果键值小于中间值，可确定要查找的键值在前半段；如果键值大于中间值，可确定要查找的键值在后半段。然后对前半段(后半段)进行分割，将其分成两等份，再对比键值。如此循环比较、分割，直到找到数据或者确定数据不存在为止。折半查找的缺点是只适用于已经初步排序好的数列；优点是查找速度快。

生活中也有类似于折半查找的例子，例如，猜数字游戏。在游戏开始之前，首先会给出一定的数字范围(例如0~100)，并在这个范围内选择一个数字作为需要被猜的数字。然后让用户去猜，并根据用户猜的数字给出提示(如猜大了或猜小了)。用户通常的做法就是先在大范围内随意说一个数字，然后提示猜大了/猜小了，这样就缩小了猜数字的范围，慢慢地就猜到了正确的数字，如下图所示。这种做法与折半查找法类似，都是通过不断缩小数字范围来确定数字，如果每次猜的范围值都是区间的中间值，就是折半查找算法了。

例如，已经有 排序好 的数列：12、45、56、66、77、80、97、101、120，要查找的数据是 101，用折半查找步骤如下：

步骤1：将数据列出来并找到中间值 77，将 101 与 77 进行比较，如下图所示。

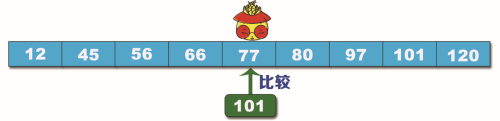
步骤2：将 101 与 77 进行比较，结果是 101 大于 77，说明要查找的数据在数列的右半段。此时不考虑左半段的数据，对在右半段的数据再进行分割，找中间值。这次中间值的位置在 97 和 101 之间，取 97，将 101 与 97 进行比较，如下图所示。

步骤3：将 101 与 97 进行比较，结果是 101 大于 97，说明要查找的数据在右半段数列中，此时不考虑左半段的数据，再对剩下的数列分割，找中间值，这次中间值位置是 101，将 101 与 101 进行比较，如下图所示。

步骤4：将 101 与 101 进行比较，所得结果相等，查找完成。说明：如果多次分割之后没有找到相等的值，表示这个键值没有在这个数列中。

从折半法查找的步骤来看，明显比顺序查找法的次数少，这就是折半查找法的优点：查找速度快。

有一条的150米线路，在这条线路上存在故障。第一天维修工已经大致锁定了几个疑似故障点，疑似故障点分别在线路的12、45、56、66、77、80、97、101、120米处。第二天维修工要在这9个疑似故障点中确定一个真正的故障点（假设真正的故障点是101米处）。维修工为了快速查找此故障点，就在每段数据的中间位置开始排查。

例如，第一次选择在77米处的疑似故障点接通电路，发现接通，他判断此故障在77米之后的位置；第二次取97米处的疑似故障点，发现也接通了，说明在97米之后的位置；第三次取101米处的位置，再次接通线路，发现未接通，说明此处是真正的故障点。此次查找经历了3次，将真正故障点找到。具体代码如下：

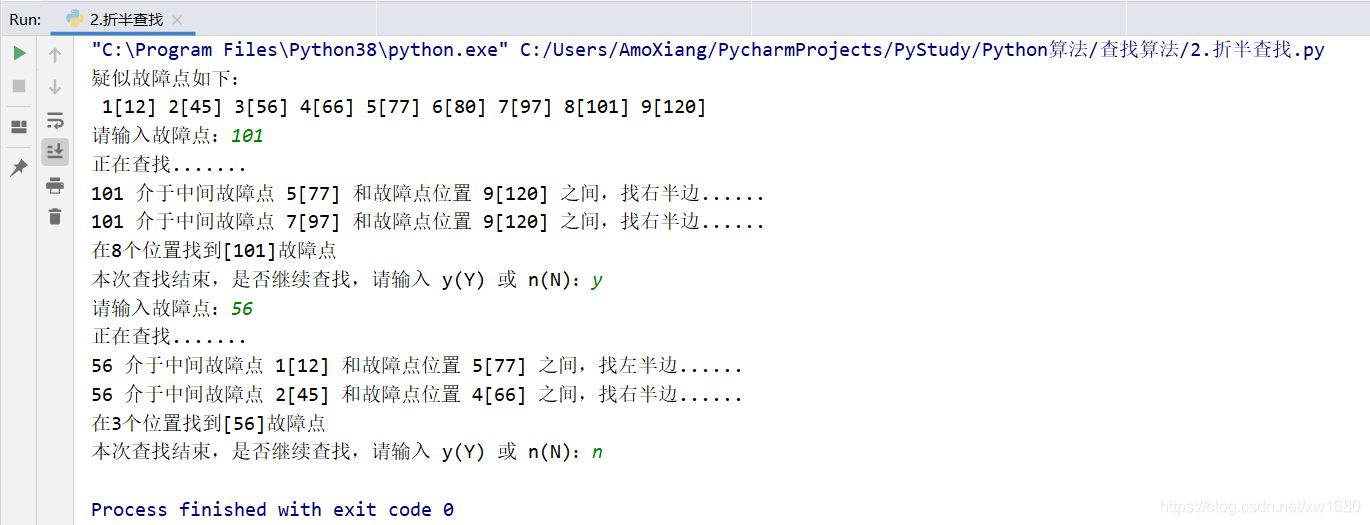
 def search(data, num): """ 定义查找函数：该函数使用的是折半查找算法 :param data: 原数列data :param num: 键值num :return: """ low = 0 # 定义变量用来表示低位 high = len(data) - 1 # 定义变量用来表示高位 print("正在查找.......") # 提示 while low <= high and num != -1: mid = int((low + high) / 2) # 取中间位置 if num < data[mid]: # 判断数据是否小于中间值 # 输出位置在数列中的左半边 print(f"{num} 介于中间故障点 {low + 1}[{data[low]}] 和故障点位置 {mid + 1}[{data[mid]}] 之间，找左半边......") high = mid - 1 # 最高位变成了中间位置减1 elif num > data[mid]: # 判断数据是否大于中间值 # 输出位置在数列中的右半边 print(f"{num} 介于中间故障点 {mid + 1}[{data[mid]}] 和故障点位置 {high + 1}[{data[high]}] 之间，找右半边......") low = mid + 1 # 最低位变成了中间位置加1 else: # 判断数据是否等于中间值 return mid # 返回中间位置 return -1 # 自定义函数到此结束 inp_num = 0 # 定义变量，用来输入键值 num_list = [12, 45, 56, 66, 77, 80, 97, 101, 120] # 定义数列 print("疑似故障点如下：") for index, ele in enumerate(num_list): print(f" {index + 1}[{ele}]", end="") # 输出数列 print("") flag = True # 开关，用来管控是否多次查找 while flag: # 循环查找 inp_num = int(input("请输入故障点：").strip()) # 输入查找键值 if inp_num == -1: # 判断键值是否是-1 break # 若为-1，跳出循环 即结束程序 result = search(num_list, inp_num) # 调用自定义的查找函数——search()函数 if result == -1: # 判断查找结果是否是-1 print(f"没有找到[{inp_num}]故障点") # 若为-1，提示没有找到值 else: # 若不为-1，提示查找位置 print(f"在{result + 1}个位置找到[{num_list[result]}]故障点") char = input("本次查找结束，是否继续查找，请输入 y(Y) 或 n(N)：").strip() if char.upper() == "N": flag = False

程序执行结果如下图所示：

三、插补查找算法

插补查找算法又称为插值查找，它是折半查找算法的改进版。插补查找是按照数据的分布，利用公式预测键值所在的位置，快速缩小键值所在序列的范围，慢慢逼近，直到查找到数据为止。根据描述来看，插值查找类似于平常查英文字典的方法。例如，在查一个以字母 D 开头的英文单词时，决不会用折半查找法。根据英文词典的查找顺序可知，D 开头的单词应该在字典较前的部分，因此可以从字典前部的某处开始查找。键值的索引计算，公式如下：

 middle=left+(target-data[left])/(data[right]-data[left])*(right-left)

参数说明：

1. middle：所求的边界索引。
2. left：最左侧数据的索引。
3. target：键值(目标数据)。
4. data[left]：最左侧数据值。
5. data[right]：最右侧数据值。
6. right：最右侧数据的索引。

例如，已经有排序好的数列：34、53、57、68、72、81、89、93、99。要查找的数据是 53，使用插补查找法步骤如下：

步骤1：将数据列出来并利用公式找到边界值，计算过程如下：

将各项数据带入公式：

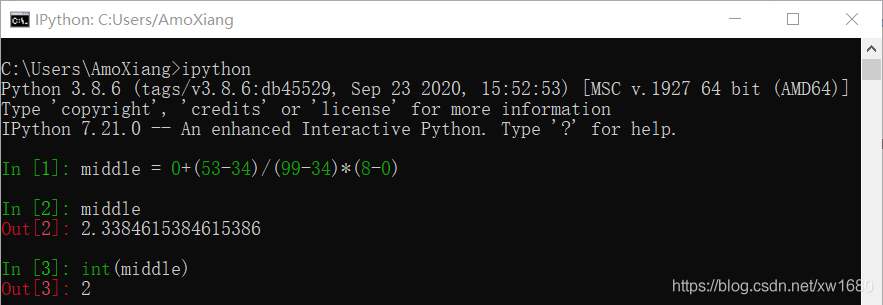
将数据取整，因此所求索引是 2，对应的数据是 57，将查找目标数据 53 与 57 进行比较，如下图所示。

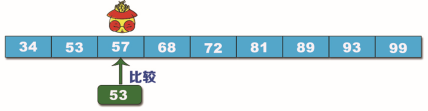
步骤2：将 53 与 57 进行比较，结果是 53 小于 57，所以查找 57 的左半边数据，不用考虑右半边的数据，索引范围缩小到 0 和 2 之间，公式带入：

取整之后索引是 1，对应的数据是 53，将查找目标数据 53 与 53 进行比较，如下图所示：

步骤3：将 53 与 53 进行比较，所得结果相等，查找完成。说明：如果多次分割之后没有找到相等的值，表示这个键值没有在这个数列中。

通过上述的步骤1就能看出，插补查找算法比折半查找算法的取值范围更小，因此它的速度要比折半法查找快，这就是插补查找算法的优点。

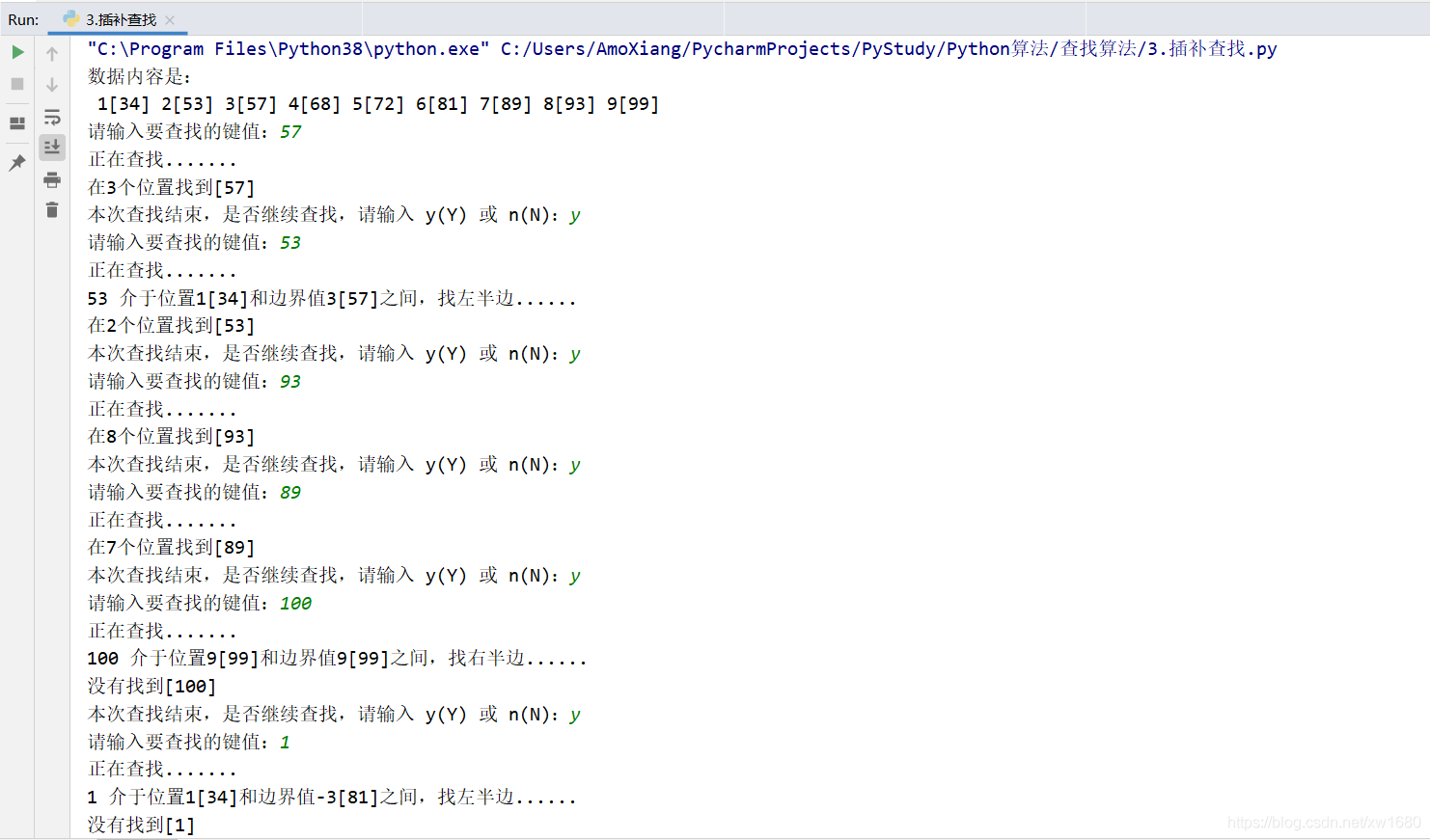
用户可以随意输入一组数据，例如本实例输入一组数据：34、53、57、68、72、81、89、93、99。在这组数据中用插补查找法分别查找数据 57、53、93、89、100，且显示每次查找的过程。用 Python 代码实现此过程，具体代码如下：

 def insert_search(data, num): """ 自定义查找函数：该函数使用的是插补查找算法 :param data: 原数列data :param num: 键值num :return: """ # 计算 left_index = 0 # 最左侧数据的索引 right_index = len(data) - 1 # 最右侧数据的索引 print("正在查找.......") # 提示 while left_index <= right_index: # 使用公式计算出索引值 middle = left_index + (num - data[left_index]) / (data[right_index] - data[left_index]) * ( right_index - left_index) # 取整 middle = int(middle) # print(middle) if num == data[middle]: return middle # 如果键值等于边界值，返回边界位置 elif num < data[middle]: # 输出位置在数列中的左半边 print(f"{num} 介于位置{left_index + 1}[{data[left_index]}]和边界值{middle + 1}[{data[middle]}]之间，找左半边......") right_index = middle - 1 # 如果键值小于边界值，最右边数据索引等于边界位置减1 else: # 输出位置在数列中的左半边 print(f"{num} 介于位置{middle + 1}[{data[middle]}]和边界值{right_index + 1}[{data[right_index]}]之间，找右半边......") left_index = middle + 1 # 如果键值大于边界值，最左边数据索引等于边界位置加1 return -1 # 自定义函数到此结束 inp_num = 0 # 定义变量，用来输入键值 num_list = [34, 53, 57, 68, 72, 81, 89, 93, 99] # 定义数列 print("数据内容是：") for index, ele in enumerate(num_list): print(f" {index + 1}[{ele}]", end="") # 输出数列 print("") flag = True # 开关，用来管控是否多次查找 while flag: # 循环查找 inp_num = int(input("请输入要查找的键值：").strip()) # 输入查找键值 result = insert_search(num_list, inp_num) # 调用自定义的查找函数——insert_search()函数 if result == -1: # 判断查找结果是否是-1 print(f"没有找到[{inp_num}]") # 若为-1，提示没有找到值 else: # 若不为-1，提示查找位置 print(f"在{result + 1}个位置找到[{inp_num}]") char = input("本次查找结束，是否继续查找，请输入 y(Y) 或 n(N)：").strip() if char.upper() == "N": flag = False

程序执行结果如下图所示：

四、哈希查找算法

哈希查找算法是使用哈希函数来计算一个键值所对应的地址，进而建立哈希表格，然后利用哈希函数来查找到各个键值存放在表格中的地址。简单来说，就是把一些复杂的数据，通过某种函数映射(与数学中的映射概念一样)关系，映射成更加易于查找的方式。哈希查找算法的查找速度与数据多少无关，完美的哈希查找算法一般都可以做到一次读取完成查找。

就像生活中，要想找到自己想要的物品，最好的办法就是把该物品固定在某个地方，每次需要用到它的时候就去对应的地方找，用完之后再放回原处。哈希查找法就是这样的一种算法，例如，在一本书中查找内容，首先翻开这本书的目录，然后在目录上找到想要的内容，最后直接根据对应的页码就能找到所需要的内容。

哈希查找算法具有保密性高的特点，因此哈希查找算法常被应用在数据压缩和加解密方面。常见的哈希算法有除留取余法、平方取中法以及折叠法。在讲解这三种算法之前，首先需要了解 哈希表 和 哈希函数 的概念。

1. 哈希表和哈希函数

哈希表是存储键值和键值所对应地址的一种数据集合。哈希表中的位置，一般称为槽位，每个槽位都能保存一个数据元素并以一个整数命名(从 0 开始)。这样我们就有了0号槽位、1号槽位等。起始时，哈希表里没有数据，槽位是空的，这样在构建哈希表时，可以把槽位的值都初始化成 None，如下图所示。

这是一个大小为 11 的哈希表，或者说有 n 个槽位的哈希表，n 为0~10。上图中的元素和保存的槽位之间的映射关系，称为哈希函数。哈希函数接受一个元素作为参数，返回一个0到n-1的整数作为槽位名。说明：每种哈希算法的哈希函数和哈希表，会在每种哈希算法中介绍。

2. 除留余数法

除留余数法是哈希算法中最简单的一种算法。它是将每个数据除以某个常数后，取余数来当索引。除留取余法所对应的哈希函数形式如下：

 h(item)=item % num

参数说明：

• item：每个数据。
• num：一个常数，一般会选择一个质数，如下面的例子中取质数 11。

例如，将整数集：54、26、93、17、77、31 中每个数据都除以 11，所得的余数作为哈希值，哈希值如下表所示。

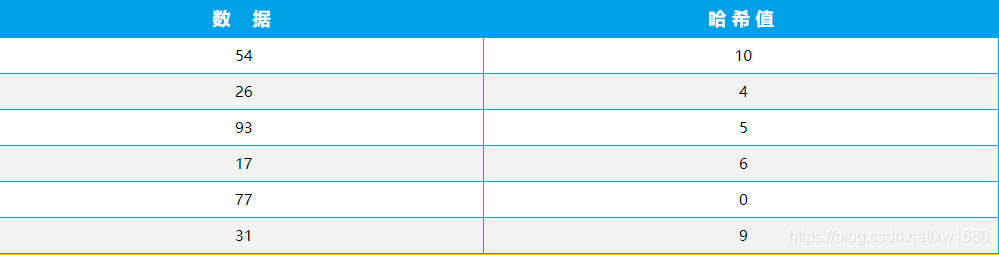
注意：除留余数法一般以某种形式存于所有哈希函数中，因为它的运算结果一定在槽位范围内。哈希值计算出来之后，就要把元素插入到哈希表中指定的位置，如下图所示。

则对应的哈希函数也得到了哈希值，如：h(54)=10，h(26)=4，h(93)=5，h(17)=6，h(77)=0，h(31)=9。

3. 折叠法

对给定的数据集，哈希函数将每个元素映射为单个槽位，称为 完美哈希函数。但是对于任意一个数据集合，没有系统能构造出完美哈希函数。例如，在上述除留余数法的例子中再加上一个数据 44，该数字除以 11 后，得到的余数是 0，这与数据 77 的哈希值相同。遇到这种情况时，解决办法之一就是扩大哈希表，但是这种做法太浪费空间。因此又有了扩展除留取余数的方案，也就是折叠法。

折叠法是将数据分成一串数据，先将数据拆成几部分，再把它们加起来作为哈希地址。例如，有这样一串数据：，将这串数据中的数字两两分一组，如下图所示：

然后将拆的数据进行相加，如下图所示：

相加之后得到的数值就是这串数据的哈希地址，如果设定槽位是 11，用除留余数法将哈希地址除以 11，得到的值是 6，而数据 6 就是这串数据的哈希值，这种做法称为 移动折叠法。

有些折叠法多了一步，就是在相加之前，对数据进行奇数或偶数反转，再将反转后的数字相加。下图所示就是将奇数反转的过程，再将反转后的数据相加，得到的 159 也称为哈希地址。

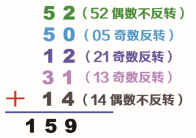
此时设定槽位是 11，将哈希地址除以 11，得到的值是 5，数据 5 就是这个数据的哈希值。接下来介绍将偶数反转的情况，如下图所示。

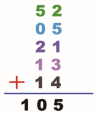
将上图中反转后的数据相加，得到的 105 也称为哈希地址。如果设定槽位是 11，除留余数法将哈希地址除以 11，得到的值是 6，数据 6 就是这个数据的哈希值。奇数/偶数反转这种折叠法称为 边界折叠法。

4. 平方取中法

平方取中法是先将各个数据平方，将平方后数据取中间的某段数字作为索引，例如，对于整数集 54，26，93，17，77，31，平方取中法如下：

步骤1：先将各个数据平方，得到的值如下：

54=2916
26=676
93=8649
17=289
77=5929
31=961

步骤2：取以上平方值的中间数，即取十位和百位，得到该整数集中数据的哈希地址分别为：

91 67 64 28 92 96

步骤3：若设置槽位是 11，将步骤 2 得到的数据分别除以 11 留余数，得到的哈希值分别为：

3 1 9 6 4 8

得到的对应关系如下图所示：

5. 碰撞与溢出问题

哈希算法的理想情况是所有数据经过哈希函数运算后得到不同的值，但是在实际情况中即使得到的哈希值不同，也有可能得到相同的地址，这种问题被称为 碰撞问题。使用哈希算法，将数据放到哈希表中存储数据的对应位置，若该位置满了，就会溢出，这种问题被称为 溢出问题。存在问题就需要解决问题，如何解决碰撞问题与溢出问题很重要。由于常见的解决问题方法有多种，故在后续博文中进行更新。

实例：用哈希查找算法查找七色光颜色。具体代码如下：

 class HashTable(object): # 创建哈希表 def __init__(self): self.size = 11 # 哈希表长度 self.throw = [None] * self.size # 哈希表数据键初始化 self.data = [None] * self.size # 哈希表数据值初始化 # 假定最终将有一个空槽，除非 key 已经存在于 self. throw中。它计算原始 # 哈希值，如果该槽不为空，则迭代 rehash 函数，直到出现空槽。如果非空槽已经包含key， # 则旧数据值将替换为新数据值 def put(self, key, value): # 输出键值 hashvalue = self.hashfunction(key, len(self.throw)) # 创建哈希值 if self.throw[hashvalue] is None: self.throw[hashvalue] = key # 将key值给哈希表的throw self.data[hashvalue] = value # 将value值给哈希表的data else: if self.throw[hashvalue] == key: self.data[hashvalue] = value else: nextslot = self.rehash(hashvalue, len(self.throw)) while self.throw[nextslot] is not None and self.throw[nextslot] != key: nextslot = self.rehash(nextslot, len(self.throw)) if self.throw[nextslot] is None: self.throw[nextslot] = key self.data[nextslot] = value else: self.data[nextslot] = value def rehash(self, oldhash, size): return (oldhash + 1) % size def hashfunction(self, key, size): return key % size # 从计算初始哈希值开始。如果值不在初始槽中，则 rehash 用 # 于定位下一个可能的位置。 def get(self, key): startslot = self.hashfunction(key, len(self.throw)) data = None found = False stop = False pos = startslot while pos is not None and not found and not stop: if self.throw[pos] == key: found = True data = self.data[pos] else: pos = self.rehash(pos, len(self.throw)) # 回到了原点，表示找遍了没有找到 if pos == startslot: stop = True return data # 重载载 __getitem__ 和 __setitem__ 方法以允许使用 [] 访问 def __getitem__(self, key): return self.get(key) def __setitem__(self, key, value): return self.put(key, value) H = HashTable() # 创建哈希表 H[16] = "红" # 给哈希表赋值 H[28] = "橙" H[32] = "黄" H[14] = "绿" H[56] = "青" H[36] = "蓝" H[71] = "紫" print("key的数据是：", H.throw) # 输出键key print("value的数据是：", H.data) # 输出值value print("结果是:", H[28]) # 根据key=28查value print("结果是:", H[71]) # 根据key=71查value print("结果是:", H[93]) # 根据key=93查value

五、分块查找算法

分块查找是二分法查找和顺序查找的改进方法，分块查找要求索引表是有序的，对块内结点没有排序要求，块内结点可以是有序的也可以是无序的。

分块查找就是把一个大的线性表分解成若干块，每块中的节点可以任意存放，但块与块之间必须排序。与此同时，还要建立一个索引表，把每块中的最大值作为索引表的索引值，此索引表需要按块的顺序存放到一个辅助数组中。查找时，首先在索引表中进行查找，确定要找的结点所在的块。由于索引表是排序的，因此，对索引表的查找可以采用顺序查找或二分查找；然后，在相应的块中采用顺序查找，即可找到对应的结点。

想要查找的数据是 150，使用分块查找法步骤如下：

步骤1：将上图所示的数据进行分块，按照每块长度为 4 进行分块，分块情况如下图所示：

说明：每块的长度是任意指定的，博主在这里用的长度为4，读者可以根据自己的需要指定每块长度。

步骤2：选取各块中的最大关键字构成一个索引表，即选取上图所示的各块的最大值，第一块最大的值是 78，第二块最大的值是 135，第三块最大值是 155，形成的索引表如下图所示：

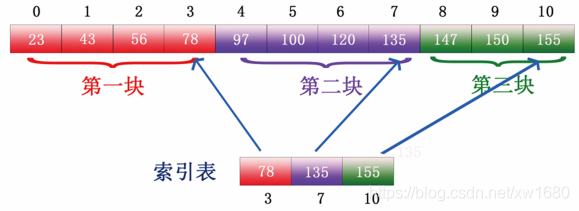
步骤3：用顺序查找或者二分查找判断想要查找数据 150 在上图所示的索引表中的哪块内容中，这里博主用的是二分查找法，即先取中间值 135 与 150 比较，如下图所示：

步骤4：结果是中间位置的数据 135 比目标数据 150 小，因此目标数据在 135 的下一块内。将数据定位在第 3 块内，此时将第 3 块内的数据取出，进行顺序比较，如下图所示：

步骤5：通过顺序查找第 3 块的内容，终于在第 9 个位置找到目标数，此时分块查找结束。

总结：至此，分块查找算法已经讲解完毕。通过和二分查找法和顺序查找法对比来看，分块查找的速度虽然不如二分查找算法，但比顺序查找算法快得多。当数据很多且块数很大时，对索引表可以采用二分查找，这样能够进一步提高查找的速度。

实例：实现分块查找算法。具体代码如下：

 def search(data, key): # 用二分查找 想要查找的数据在哪块内 length = len(data) # 数据列表长度 first = 0 # 第一位数位置 last = length - 1 # 最后一个数据位置 print(f"长度:{length} 分块的数据是:{data}") # 输出分块情况 while first <= last: mid = (last + first) // 2 # 取中间位置 if data[mid] > key: # 中间数据大于想要查的数据 last = mid - 1 # 将last的位置移到中间位置的前一位 elif data[mid] < key: # 中间数据小于想要查的数据 first = mid + 1 # 将first的位置移到中间位置的后一位 else: return mid # 返回中间位置 return False # 分块查找 def block(data, count, key): # 分块查找数据，data是列表，count是每块的长度，key是想要查找的数据 length = len(data) # 表示数据列表的长度 block_length = length // count # 一共分的几块 if count * block_length != length: # 每块长度乘以分块总数不等于数据总长度 block_length += 1 # 块数加1 print("一共分", block_length, "块") # 块的多少 print("分块情况如下：") for block_i in range(block_length): # 遍历每块数据 block_data = [] # 每块数据初始化 for i in range(count): # 遍历每块数据的位置 if block_i * count + i >= length: # 每块长度要与数据长度比较，一旦大于数据长度 break # 就退出循环 block_data.append(data[block_i * count + i]) # 每块长度要累加上一块的长度 result = search(block_data, key) # 调用二分查找的值 if result != False: # 查找的结果不为False return block_i * count + result # 就返回块中的索引位置 return False data = [23, 43, 56, 78, 97, 100, 120, 135, 147, 150, 155] # 数据列表 result = block(data, 4, 150) # 第二个参数是块的长度，最后一个参数是要查找的元素 print("查找的值得索引位置是:", result) # 输出结果

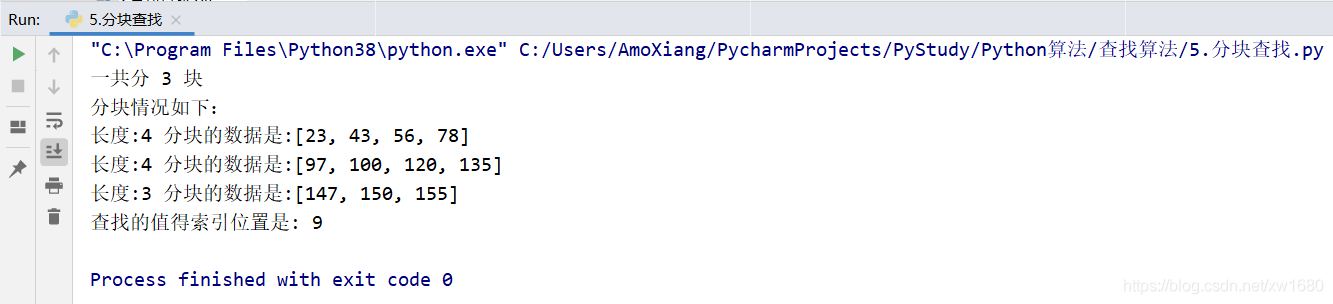
从上面的运行结果看到，当查找 150 时，查找结果完全符合上述描述的步骤。

六、斐波那契查找算法

斐波那契查找也称为黄金分割法查找，是在二分查找的基础上根据斐波那契数列进行分割，二分法是取排序好的中间值进行分割，而斐波那契查找是根据黄金分割点进行分割。想要掌握斐波那契查找，首先需要了解两个概念，一个是黄金分割点，另一个是斐波那契数列。

黄金分割点。黄金分割点是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比，其比值取其前三位数字的近似值是 0.618。0.618 是一个神奇的数字，在建筑学和设计学等方面，按照按此比例设计的造型就会十分美丽，因此称为黄金分割。这个分割点就叫作黄金分割点。斐波那契数列。斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、34、55……，在数学上，斐波那契被递归方法如下定义：F(1)=1，F(2)=1，F(n) = F(n-1)+F(n-2) (n>=2)。斐波那契数列越往后，前后两项的比值越接近 0.618，也就是黄金比例的比值。

说明：假如待查找列表长度为 F(n)，不考虑 mid 的情况下，左边为 F(n - 1)，右边为 F(n -2)，考虑 mid 的情况下要不左边是 F(n-1) - 1 或者右边是 F(n - 2) - 1，逻辑不好写，如果待查找长度为 F(n) - 1，mid = low + (F(n - 1) - 1) 则不存在这样的问题。

用斐波那契查找法步骤如下：

说明：斐波那契查找也和二分查找法一样，需要在查找前，将数列排序好。

步骤1：先来看一下原始数据的长度，如上图所示长度是 9，再来看斐波那契数列 1、1、2、3、5、8、13、21、34、55····，从数据来看，最接近的数字是 13，因此将原始数据的长度扩展到 13，用上图的最后一个数据 53 补齐。如下图所示：

步骤2：接下来得找查找算法里的中间值了，首先假设创建斐波那契数列为 F(n)，斐波那契数列的规律 F(n)= F(n-1)+ F(n-2)，上图已经将原数列长度补充到 13，在斐波那契数列中 13=8+5，即 F(6)=F(5)+F(4)，则中间是 F(5)，在斐波那契数列中 F(5)=8，因此 mid=low+F(5)-1=7。如下图所示：

步骤3：从数据上看，mid=7 对应的数据是 48，目标数据 37 比 48 小，因此再次寻找以 mid 为分割线的左侧部分数据，此时 high 的值从 8 的位置变为 mid-1 的位置，即此时 high=6，low 值不变，依然是 0。如下图所示：

步骤4：此时图中所示的数据长度变成了 7，再次找此时数据的中间值，数据长度 7 与斐波那契数列的数字 8 比较接近，8=3+5，8 在斐波那契数列中是 F(5)，即 F(5)=F(4)+F(3)，中间值是 F(4)，在斐波那契数列中 F(4)=5，此时的 mid=low+F(4)-1=4。如下图所示：

步骤5：从数据上看，mid=4 对应的数据是 22。目标数据 37 比 22 大，因此再次寻找以 mid为 分割线的右侧部分数据，此时 low 的值从 0 的位置变为 mid+1 的位置，即此时 low=5，high 值不变，依然是 6，如下图所示：

步骤6：从上图可知 high=6，最接近的斐波那契数列的数据是 8，8=3+5，8 在斐波那契数列中是 F(5)，即 F(5)=F(4)+F(3)，虚拟中间值是 F(4)，因为是在中间值的右侧寻找，因此需要计算 F(n-2)=F(4-2)=F(2)，在斐波那契数列中 F(2)=2，此时的 mid=low+F(2)-1=5+1=6，如下图所示：

步骤7：从数据上看，mid=4 对应的数据是 37，目标数据 37 等于中间值 37，此时返回寻找的位置，即返回 mid 的位置。如果计算 mid 的值大于 high 的值，就之间返回 high 的值。此时已经用斐波那契查找完成寻找目标数据 37 的任务。

总结来说：斐波那契查找与二分查找很相似，它是根据斐波那契序列的特点对有序表进行分割的。它要求开始表中记录的个数为某个斐波那契数小 1，即 k=F(n)-1;开始将 n 值与第 F(n-1) 位置的记录进行比较 (即 mid=low+F(n-1)-1)，比较结果也分为三种：

相等，mid 位置的元素即为所求。n > F(n-1) 位置的记录，low=mid+1，n-=2。说明：low=mid+1 说明待查找的元素在 [mid+1,hign]（即右侧）范围内，n-=2 说明范围 [mid+1,high] 内的元素个数为 k-（F(n-1))= F(n)-1-F(n-1)=F(n)-F(n-1)-1=F(n-2)-1 个，所以可以递归的应用斐波那契查找。n < F(n-1)位置的记录 ，high=mid-1，n-=1。说明：low=mid+1 说明待查找的元素在 [low,mid-1]（即左侧）范围内，k-=1 说明范围 [low,mid-1] 内的元素个数为 F(k-1)-1 个，所以可以递归的应用斐波那契查找。

接下来用Python代码来实现以上描述的斐波那契查找。

 def fibonacci_search(data, key): # 需要一个现成的斐波那契列表。其最大元素的值必须超过查找表中元素个数的数值 F = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765] low = 0 # 低位 high = len(data) - 1 # 高位 # 为了使得查找表满足斐波那契特性，在表的最后添加几个同样的值 # 这个值是原查找表的最后那个元素的值 # 添加的个数由F[k]-1-high决定 k = 0 while high > F[k] - 1: k += 1 i = high # 将i定位到high的位置 while F[k] - 1 > i: # 添加数据 data.append(data[high]) # 追加到high之后的位置上 i += 1 print("添加后的数据", data) # 输出追加后的数据 # 算法主逻辑，count用于展示循环的次数 while low <= high: # 满足低位小于等于高位 # 为了防止F列表下标溢出，设置if和else if k < 2: mid = low else: mid = low + F[k - 1] - 1 print("低位位置：%s, 中间位置：%s,高位位置：%s" % (low, mid, high)) # 输出每次分割情况 if key < data[mid]: # 目标数据小于中间值数据，在左侧寻找 high = mid - 1 # 高位位置移到mid-1的位置 k -= 1 # 下标k此时减1 elif key > data[mid]: # 目标数据大于中间值数据，在右侧寻找 low = mid + 1 # 低位位置移到mid+1的位置 k -= 2 # 下标k此时减2 else: # 否则 if mid <= high: # 中间值小于等于mid return mid # 此时的结果是mid就是目标值得位置，返回mid即可 else: # 如果mid大于了高位位置值 return high # 此时的结果直接返回high的值 return False # 验证数据 data = [9, 10, 13, 15, 22, 29, 37, 48, 53] # 数据列表 key = int(input("请输入想要查找的数据：")) result = fibonacci_search(data, key) # 调用斐波那契查找函数 print("目标数据", key, "的位置是", result) # 输出结果

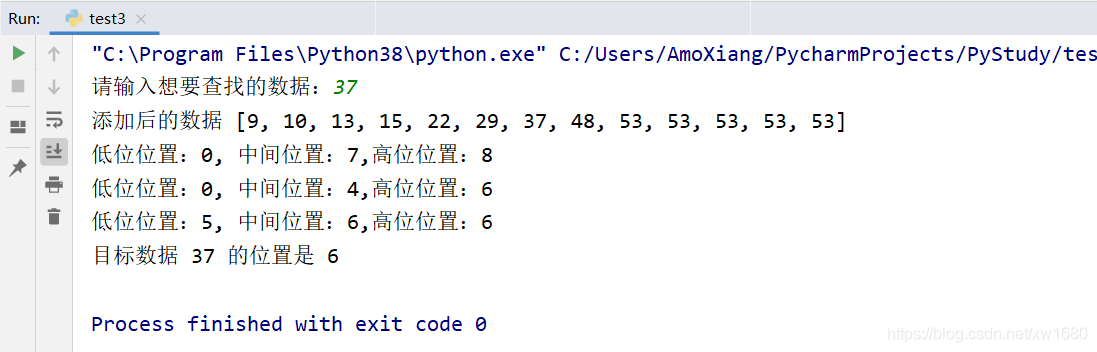
从上图中的运行结果看到，当查找 37 时，查找结果完全符合上述描述的步骤。如果想要进行其他数据的查找，都可以通过斐波那契查找算法实现，这里就不一一讲解了。

七、六种查找算法的时间复杂度

在第 1~6 节中介绍了六种查找算法，本节就用大 O 表示法来比较一下这四种查找算法的时间复杂度。先来总结这四种查找算法的基本思想：

• 顺序查找算法：按照数据的顺序一项一项逐个查找，所以不管数据顺序如何，都要从头到尾的遍历一次。速度比较慢，它的时间复杂度是 T=O(n)。
• 二分查找算法：将数据分割成两等份，然后用键值(要查找的数据)与中间值比较，逐渐缩短查找范围。速度比顺序查找快，它的时间复杂度是 T=O(log n)。
• 插补查找算法：按照数据的分布，利用公式预测键值所在的位置，快速缩小键值所在序列的范围，慢慢逼近，直到查找到数据为止，这种算法比二分查找速度还快，它的时间复杂度是 T=O(log log(n))。
• 分块查找算法：要求是顺序表，它是顺序查找的一种改进方法，它的时间复杂度是 T= O(log2(m)+N/m)。
• 斐波那契查找算法：斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。用键值(要查找的数据)与黄金分割点进行比较，逐渐缩短查找范围。它的时间复杂度是 T=O(log 2n)。
• 哈希查找算法：把一些复杂的数据，通过某种函数映射(概念和数学中映射一样)关系，映射成更加易于查找的方式。这种方法速度最快，它的时间复杂度是 T=O(1)。

到此这篇关于Python 语言实现六大查找算法的文章就介绍到这了,更多相关python查找算法内容请搜索本网站以前的文章或继续浏览下面的相关文章希望大家以后多多支持本网站！

您可能感兴趣的文章:

• PHP局部异常因子算法-Local Outlier Factor(LOF)算法的具体实现解析
• java排序算法图文详解
• Java实现雪花算法的原理和实战教程
• c++ Bellman-Ford算法的具体实现
• Java实现常见排序算法的优化
• 异常点/离群点检测算法——LOF解析