目录
- 前言
- 简介
- 区别
- 其他非线性关系
- 结论
前言
相关系数是用以反映变量之间的相关关系程度的统计指标。
其取值范围是[-1,1],当取值为0时表示不相关,取值为[-1,0)表示负相关,取值为(0,-1],表示负相关。
目前常用的两种相关性系数为皮尔森相关系数(Pearson)和斯皮尔曼等级相关系数(Spearman)
简介
1.皮尔森相关系数评估两个连续变量之间的线性关系。
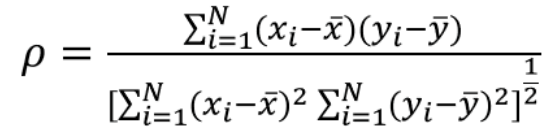
其中:
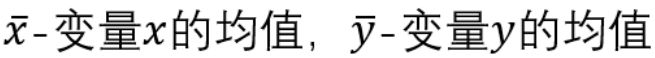
-1 ≤ p ≤ 1
p接近0代表无相关性
p接近1或-1代表强相关性
2.斯皮尔曼相关系数评估两个连续变量之间的单调关系。在单调关系中,变量趋于一起变化,但不一定以恒定速率变化。
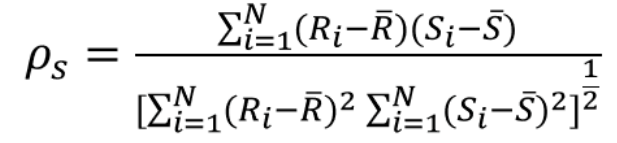
其中:

N是观测值的总数量
斯皮尔曼另一种表达公式:
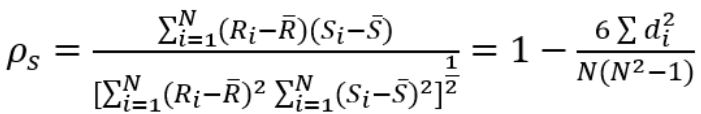
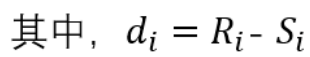
表示二列成对变量的等级差数。
区别
Pearson和Spearman相关系数的范围可以从-1到+1。
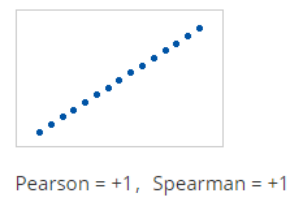
当Pearson相关系数为+1时,意味着,当一个变量增加时,另一个变量增加一致量。
这形成了一种递增的直线。
在这种情况下,Spearman相关系数也是+1。
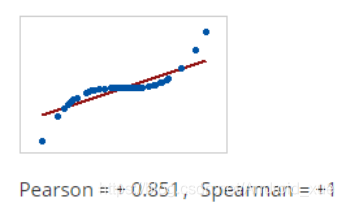
如果关系是一个变量在另一个变量增加时增加,但数量不一致,则Pearson相关系数为正但小于+1。
在这种情况下,斯皮尔曼系数仍然等于+1。
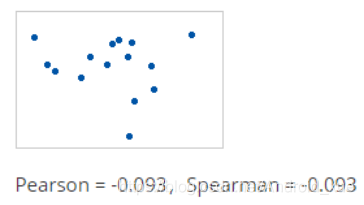
当关系是随机的或不存在时,则两个相关系数几乎为零。
如果关系递减的直线,那么两个相关系数都是-1。

如果关系是一个变量在另一个变量增加时减少,但数量不一致,则Pearson相关系数为负但大于-1。
在这种情况下,斯皮尔曼系数仍然等于-1
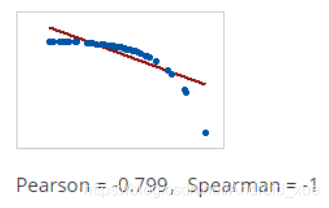
相关值-1或1意味着精确的线性关系,如圆的半径和圆周之间的关系。
然而,相关值的实际价值在于量化不完美的关系。
发现两个变量是相关的经常通知回归分析,该分析试图更多地描述这种类型的关系。
其他非线性关系
Pearson相关系数仅评估线性关系。Spearman相关系数仅评估单调关系。
因此,即使相关系数为0,也可以存在有意义的关系。
检查散点图以确定关系的形式。
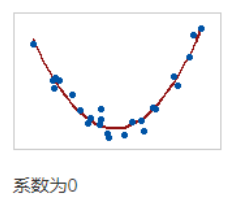
该图显示了非常强的关系。
Pearson系数和Spearman系数均约为0。
结论
皮尔森评估的是两个变量的线性关系,而斯皮尔曼评估的两变量的单调关系。
因此,斯皮尔曼相关系数对于数据错误和极端值的反应不敏感。
以上为个人经验,希望能给大家一个参考,也希望大家多多支持本网站。
您可能感兴趣的文章:
- Python+pandas计算数据相关系数的实例
- 详解Python进行数据相关性分析的三种方式
- python皮尔逊相关性数据分析分析及实例代码
