Python曲线拟合多项式深入详解

目录

• np.polyfit 多项式拟合
• 例1
• 例2
• curve_fit () 自定义函数拟合
• scipy.interpolate.interpnd 插值拟合

np.polyfit 多项式拟合

在python中，Numpy.polyfit()是一个在多项式函数内拟合数据的方法。当最小二乘法的拟合条件很差时，polyfit会发出RankWarning。

对散点进行多项式拟合并打印出拟合函数以及拟合后的图形程序如下

例1

在这个程序中，首先，导入matplotlib和numpy库。设置x、y、p和t的值。然后，使用这个x、y、p和t的值，通过拟合绘制多项式。

import numpy as np import matplotlib.pyplot as plt np.random.seed(46) x = np.linspace(0, 1, 25) y = np.cos(x) + 0.3 * np.random.rand(25) p = np.poly1d(np.polyfit(x, y, 4)) t = np.linspace(0, 1, 250) plt.plot(x, y, 'o', t, p(t), '-') plt.show()

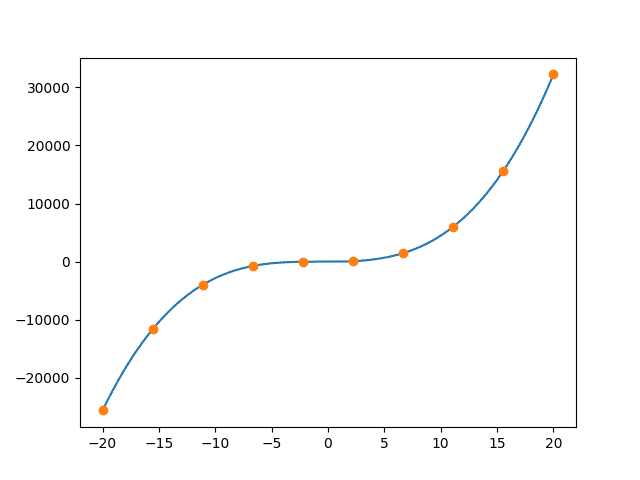
例2

在这个程序中，也是如此，首先，导入matplotlib和numpy库。设置x和y的值。然后，计算多项式并设置x和y的新值。一旦完成，使用函数polyfit()拟合多项式。

import numpy as np import matplotlib.pyplot as plt np.random.seed(12) x = np.linspace(-20, 20, 10) y = 3.6 * pow(x, 3) + 8.3 * pow(x, 2) + 5.1 * pow(x, 1) + 5 func = np.polyfit(x, y, 4) xn = np.linspace(-20, 20, 1000) yn = np.poly1d(func) plt.plot(xn, yn(xn), x, y, 'o') plt.show()

curve_fit () 自定义函数拟合

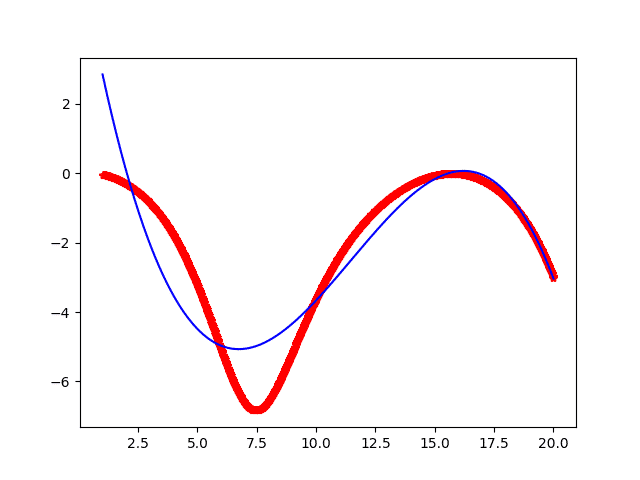
能拟合的函数不止下面这些，只要你写出想要使用的函数的表达式，就可以得到函数的参数！！！

import numpy as np # NumPy https://numpy.org/ import matplotlib.pyplot as plt # Matplotlib https://matplotlib.org/ from scipy.optimize import curve_fit # https://www.scipy.org/ # 三次 - 跟前面所说的poly_fit一个意思 def func_poly_3(x, a, b, c , d): return a*x*x*x + b*x*x + c*x + d # 幂函数 def func_power(x, a, b): return xa + b # 指数函数 def func_exp(x, a, b): return ax + b def Hyperb(x, a1, a2, qi): y = qi / np.power(1 + a1 * a2 * x, 1 / a2) return y xdata=[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.85435, 1., 1., 1., 1., 1., 1., 1., 2.0029326, 2.0, 2.0, 2.058651, 2.0, 2.0, 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 3.0058651, 3.0, 3.0, 3.0, 3.0, 3.0, 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 4.0087977, 4.0, 4.0, 4.0, 4.083089, 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4.28739, 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 5.0, 5.030303, 5.0, 5.0, 5.0, 5., 5., 5.14174, 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 6.0, 6.0, 6.0, 6.0, 6.0, 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 7.0, 7.0, 7.054741, 7.0, 7.0, 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 8.001955, 8.0, 8.0, 8.0, 8.0, 8.0, 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8.42913, 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 9.0048876, 9.0, 9.0, 9.0, 9.0, 9.0, 9., 9., 9., 9., 9., 9., 9., 9., 9., 9.28348, 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 10.00782, 10.026393, 10.044966, 10.063539, 10.082111, 10., 10., 10.13783, 10., 10., 10., 10., 10., 10., 10.26784, 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10.5, 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10.73216, 10., 10., 10., 10., 10., 10., 10.86217, 10., 10., 10., 10., 10., 10., 10.99218, 11.010753, 11.029326, 11.047898, 11.066471, 11.085044, 11., 11.12219, 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11.4565, 11., 11., 11., 11., 11., 11., 11.58651, 11., 11., 11., 11., 11., 11., 11.71652, 11., 11., 11., 11., 11., 11., 11.84653, 11., 11., 11., 11., 11., 11., 11.97654, 11., 12.013685, 12.032258, 12.050831, 12.069404, 12.087977, 12., 12., 12., 12., 12., 12., 12., 12., 12., 12., 12., 12.31085, 12., 12., 12., 12., 12., 12., 12.44086, 12., 12., 12., 12., 12., 12., 12.57087, 12., 12., 12., 12., 12., 12., 12.70088, 12., 12., 12., 12., 12., 12., 12.83089, 12., 12., 12., 12., 12., 12., 12., 12., 12., 13.016618, 13.035191, 13.053763, 13.072336, 13.090909, 13., 13., 13., 13.1652, 13., 13., 13., 13., 13., 13., 13.29521, 13., 13., 13., 13., 13., 13., 13.42522, 13., 13., 13., 13., 13., 13., 13.55523, 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 14.000978, 14.01955, 14.038123, 14.056696, 14.075269, 14.093842, 14., 14., 14.14956, 14., 14., 14., 14., 14., 14., 14.27957, 14., 14., 14., 14., 14., 14., 14.40958, 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14.8739, 14., 14., 14., 14., 14., 14., 15.00391, 15.022483, 15.041056, 15.059629, 15.078201, 15.096774, 15., 15.13392, 15., 15., 15., 15., 15., 15., 15.25, 15.26393, 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15.59824, 15., 15., 15., 15., 15., 15., 15.72825, 15., 15., 15., 15., 15., 15., 15.85826, 15., 15., 15., 15., 15., 15., 15.98827, 16.006843, 16.025415, 16.043988, 16.062561, 16.081134, 16.099707, 16.11828, 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16.45259, 16., 16., 16., 16., 16., 16., 16.5826, 16., 16., 16., 16., 16., 16., 16.71261, 16., 16., 16., 16., 16., 16., 16.84262, 16., 16., 16., 16., 16., 16., 16.97263, 16., 17.009775, 17.028348, 17.046921, 17.065494, 17.084066, 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17.30694, 17., 17., 17., 17., 17., 17., 17.43695, 17., 17., 17., 17., 17., 17., 17.56696, 17., 17., 17., 17., 17., 17., 17.69697, 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 18.012708, 18.031281, 18.049853, 18.068426, 18.086999, 18., 18., 18., 18.16129, 18., 18., 18., 18., 18., 18., 18.2913, 18., 18., 18., 18., 18., 18., 18.42131, 18., 18., 18., 18., 18., 18., 18.55132, 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18.88563, 18., 18., 18., 18., 18., 18., 19.01564, 19.034213, 19.052786, 19.071359, 19.089932, 19., 19., 19.14565, 19., 19., 19., 19., 19., 19., 19.27566, 19., 19., 19., 19., 19., 19., 19.40567, 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19.73998, 19., 19., 19., 19., 19., 19., 19.86999, 19., 19., 19., 19., 19., 19., 20.0] ydata=[-0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -1.0069907, -1.0, -1.0, -1.0, -1.0, -1.0, -1.099558, -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -2.0, -2.0, -2.0, -2.0, -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2.47544, -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -3.017392, -3.0, -3.0, -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -4.0, -4.0, -4.0, -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -5.0, -5.0, -5.0, -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -6.0080597, -6.037272, -6.0, -6.0, -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6.0, -6.0, -6.0, -6.0024454, -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5.0, -5.0, -5.0, -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4.0, -4.0, -4.0, -4.0019828, -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3.0, -3.0, -3.0, -3.0, -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2.65677, -2.63505, -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2.1479, -2., -2., -2.0, -2.0, -2.0, -2.0, -2.0, -1., -1.98157, -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.015459, -1.0035181, -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -1.0028149, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -2.0, -2.0, -2.0, -2.0, -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -3.0] popt, pcov = curve_fit(func_poly_3, xdata, ydata, method='lm',maxfev = 8866) plot1 = plt.plot(np.array(xdata), ydata, 'r*', label='original values') plot2 = plt.plot(np.array(xdata), [func_poly_3(i, *popt) for i in xdata], 'b', label='curvefit values') plt.show() 

scipy.interpolate.interpnd 插值拟合

前两种都限于你得提前知道待拟合的是什么函数, 可不可以通过大量的点插值得到函数呢?

python的scipy.interpolate模块有一维插值函数interp1d，二维插值函数interp2d，多维插值函数interpnd.

在此只对一维插值做演示.

import numpy as np from scipy.interpolate import interp1d import matplotlib.pyplot as plt xdata=[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.85435, 1., 1., 1., 1., 1., 1., 1., 2.0029326, 2.0, 2.0, 2.058651, 2.0, 2.0, 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 2., 3.0058651, 3.0, 3.0, 3.0, 3.0, 3.0, 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 3., 4.0087977, 4.0, 4.0, 4.0, 4.083089, 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4.28739, 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 4., 5.0, 5.030303, 5.0, 5.0, 5.0, 5., 5., 5.14174, 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 5., 6.0, 6.0, 6.0, 6.0, 6.0, 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 6., 7.0, 7.0, 7.054741, 7.0, 7.0, 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 7., 8.001955, 8.0, 8.0, 8.0, 8.0, 8.0, 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8.42913, 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 8., 9.0048876, 9.0, 9.0, 9.0, 9.0, 9.0, 9., 9., 9., 9., 9., 9., 9., 9., 9., 9.28348, 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 9., 10.00782, 10.026393, 10.044966, 10.063539, 10.082111, 10., 10., 10.13783, 10., 10., 10., 10., 10., 10., 10.26784, 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10.5, 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10.73216, 10., 10., 10., 10., 10., 10., 10.86217, 10., 10., 10., 10., 10., 10., 10.99218, 11.010753, 11.029326, 11.047898, 11.066471, 11.085044, 11., 11.12219, 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11., 11.4565, 11., 11., 11., 11., 11., 11., 11.58651, 11., 11., 11., 11., 11., 11., 11.71652, 11., 11., 11., 11., 11., 11., 11.84653, 11., 11., 11., 11., 11., 11., 11.97654, 11., 12.013685, 12.032258, 12.050831, 12.069404, 12.087977, 12., 12., 12., 12., 12., 12., 12., 12., 12., 12., 12., 12.31085, 12., 12., 12., 12., 12., 12., 12.44086, 12., 12., 12., 12., 12., 12., 12.57087, 12., 12., 12., 12., 12., 12., 12.70088, 12., 12., 12., 12., 12., 12., 12.83089, 12., 12., 12., 12., 12., 12., 12., 12., 12., 13.016618, 13.035191, 13.053763, 13.072336, 13.090909, 13., 13., 13., 13.1652, 13., 13., 13., 13., 13., 13., 13.29521, 13., 13., 13., 13., 13., 13., 13.42522, 13., 13., 13., 13., 13., 13., 13.55523, 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 13., 14.000978, 14.01955, 14.038123, 14.056696, 14.075269, 14.093842, 14., 14., 14.14956, 14., 14., 14., 14., 14., 14., 14.27957, 14., 14., 14., 14., 14., 14., 14.40958, 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14., 14.8739, 14., 14., 14., 14., 14., 14., 15.00391, 15.022483, 15.041056, 15.059629, 15.078201, 15.096774, 15., 15.13392, 15., 15., 15., 15., 15., 15., 15.25, 15.26393, 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15., 15.59824, 15., 15., 15., 15., 15., 15., 15.72825, 15., 15., 15., 15., 15., 15., 15.85826, 15., 15., 15., 15., 15., 15., 15.98827, 16.006843, 16.025415, 16.043988, 16.062561, 16.081134, 16.099707, 16.11828, 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16.45259, 16., 16., 16., 16., 16., 16., 16.5826, 16., 16., 16., 16., 16., 16., 16.71261, 16., 16., 16., 16., 16., 16., 16.84262, 16., 16., 16., 16., 16., 16., 16.97263, 16., 17.009775, 17.028348, 17.046921, 17.065494, 17.084066, 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17.30694, 17., 17., 17., 17., 17., 17., 17.43695, 17., 17., 17., 17., 17., 17., 17.56696, 17., 17., 17., 17., 17., 17., 17.69697, 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 17., 18.012708, 18.031281, 18.049853, 18.068426, 18.086999, 18., 18., 18., 18.16129, 18., 18., 18., 18., 18., 18., 18.2913, 18., 18., 18., 18., 18., 18., 18.42131, 18., 18., 18., 18., 18., 18., 18.55132, 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18., 18.88563, 18., 18., 18., 18., 18., 18., 19.01564, 19.034213, 19.052786, 19.071359, 19.089932, 19., 19., 19.14565, 19., 19., 19., 19., 19., 19., 19.27566, 19., 19., 19., 19., 19., 19., 19.40567, 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19., 19.73998, 19., 19., 19., 19., 19., 19., 19.86999, 19., 19., 19., 19., 19., 19., 20.0] ydata=[-0.000, -9.e-16, -9.e-16, -9.e-16, 0.0, 0.0, 0.0, 0.0, -9.e-16, 0.0, 0.0, 0.0, 0.0, -1.e-15, 0.0, -9.e-16, -9.e-16, 0.0, -9.e-16, 0.0, 0.0, 0.0, -9.e-16, 0.0, 0.0, -9.e-16, -9.e-16, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, -9.e-16, 1.e-15, -9.e-16, -9.e-16, -9.e-16, -9.e-16, 0.0, 0.0, -9.e-16, 0.0, -9.e-16, -9.e-16, 0.0, -9.e-16, -9.e-16, -9.e-16, -9.e-16, 0.0, -9.e-16, -9.e-16, 0.0, 0.0, 0.0, -9.e-16, -9.e-16, 0.0, 0.0, 0.0, 0.0, 0.0, -9.e-16, 0.0, -9.e-16, -9.e-16, 0.0, 0.0, -1.e-15, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, -9.e-16, -9.e-16, 0.0, 0.0, 0.0, -0.000, -0.000, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.00, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -0., -1.0006024, -1.0076086, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.072163, -1.0, -1.0, -1.0, -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1.26594, -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1.72032, -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1.90672, -1., -1., -1., -1., -1., -1., -1., -1., -2.0046025, -2.0, -2.0, -2.0, -2.0, -2.060347, -2.0, -2.0, -2.0, -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -2., -3.0026033, -3.0, -3.0, -3.0, -3.0, -3.0, -3.0, -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3.51114, -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -3., -4.0001614, -4.0, -4.0, -4.051151, -4.068232, -4.0, -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -4., -5.0, -5.0, -5.0, -5.0, -5.092234, -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5., -5.92624, -5., -5., -5., -6.0, -6.0, -6.0, -6.0, -6.0, -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6., -6.99427, -7.0, -7.0, -7.0, -7.0, -7., -7., -7., -7., -7., -7.22943, -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -7., -8.0, -8.0, -8.0, -8.0, -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -8., -9.0017193, -9.0, -9.0, -9.0, -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -9., -10.001274, -10.029898, -10.058569, -10.087285, -10., -10., -10., -10., -10., -10., -10., -10., -10.34779, -10., -10.40618, -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -10., -11.030014, -11.060198, -11.090425, -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11., -11.76571, -11., -11.82803, -11., -11., -11., -11., -11.98446, -12.015852, -12.047278, -12.078738, -12., -12.14176] # method: 插值方法: 可选 {‘linear', ‘nearest', ‘cubic'} 之一 # ‘linear': 分段线性, ‘nearest': 最近邻点, ‘cubic': 三次样条（cubic spline）插值 func = interp1d(xdata, ydata, kind='cubic') x_new = np.linspace(start=min(xdata), stop=max(xdata), num=10) y_new = func(x_new) plot1 = plt.plot(xdata, ydata, 'r', label='original values') plt.scatter(x_new, y_new) # 此时即为平滑曲线 plt.show() 

到此这篇关于Python曲线拟合多项式深入详解的文章就介绍到这了,更多相关Python曲线拟合内容请搜索本网站以前的文章或继续浏览下面的相关文章希望大家以后多多支持本网站！

您可能感兴趣的文章:

• Python使用scipy进行曲线拟合的方法实例
• 如何利用Python拟合函数曲线详解
• Python实现批量梯度下降法(BGD)拟合曲线
• Python实现曲线拟合的最小二乘法
• python 对任意数据和曲线进行拟合并求出函数表达式的三种解决方案
• 详解用Python为直方图绘制拟合曲线的两种方法
• python 绘制拟合曲线并加指定点标识的实现